Harem Party – Installation guide
1. Download “Harem Party” game
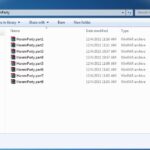
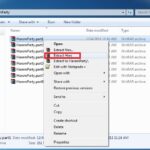
2. Right-click on first part and select “Extract here”
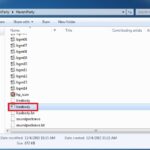
3. Once unpacking is complete, open newly created folder and start the game with lcsebody.exe
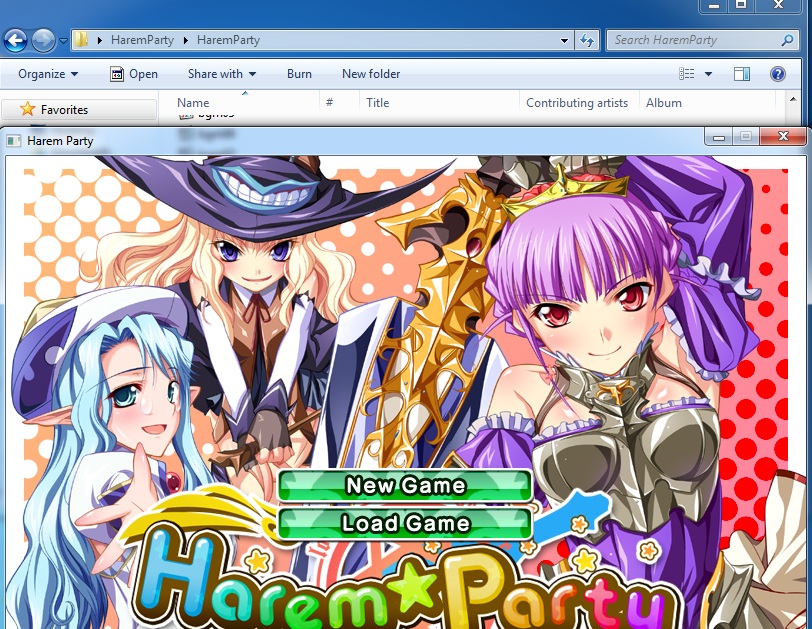
4. Enjoy the game!
1. Download “Harem Party” game
2. Right-click on first part and select “Extract here”
3. Once unpacking is complete, open newly created folder and start the game with lcsebody.exe
4. Enjoy the game!
"Cute British girl 'Lisa' embarks on a new challenge in South Korea, a small country in the Far East, with her dream of becoming a bodybuilder. As the owner of [...]
Our last summer at Seisho Music Academy―― With the 101st Seisho Festival "Starlight" coming up, we the students of the 99th class take up the challenge to perform "El Dorado", [...]
Fired from his job due to a serious mistake, Haito Kanda tries to find solace in alcohol at his favorite pub amid despair, unaware that a fateful encounter awaits. The [...]
Kyoichi Akikawa lost his family in a devastating plane crash when he was just a child. "Will it really come someday?" "Will the day ever come when I can truly [...]
"Kimi ga Nozomu Eien" returns as an Enhanced Edition! This legendary visual novel left fans emotionally wrecked for days after its release, and two decades later, its rollercoaster storyline still [...]
This is a Story of "Love" One day, Hitomi Tadehara, the best friend of Ichika Shinonome, committed suicide right before her eyes. "I'm sorry for hurting you so much, Ichika-chan." [...]
Japan Trip is a captivating visual novel that takes you on an unforgettable adventure through the bustling streets of Tokyo, where every corner holds new experiences and every encounter could [...]
Her slender and straight legs are wearing black stockings, her white shirt is wide open, her hands are soft and white, and she looks even more charming under her light [...]
You play as a young man who goes to a country house with his parents to celebrate Christmas. However, the father suddenly has to leave on business, but soon it [...]
One ordinary night, our protagonist's life takes a wild turn when he stumbles upon an ancient, mysterious book, lost in a dark alley. The book reveals age-old techniques of magical [...]
Your childhood friend is hosting a small house party to celebrate his 21st birthday and you're invited. You haven't really kept in touch with him ever since you started university [...]
On my windows10 its not responding
So, the game plays fine (just a few minutes into it) and I fixed the spacing problem by installing the “Vera” fonts to my “C” drive, all letters and punctuation are properly spaced but the lines run off to the next line in the middle of the word.
Maybe it the fact that one file was unable to be installed into C:/Windows/Fonts, and that is the very first file in the “Vera” folder. It’s “local.config”. There’s no way I know to install this file as my PC keeps saying “…does not appear to be a valid font”. The rest of the files are ok as they are all “TrueTypefontfile”.
Is this the way it should happen?
If it is, I don’t mind, at least I can understand what is being said now. But if there is a way to fix the wrap around/no wrap around problem I’d like to find out.
Also I have Windows 8.1 so there were no “install new fonts” option (that doesn’t involve fonts coming directly from Microsoft only) so I just copy and pasted it.
for admin
parts 2 and 3 are corrupted and cant be extracted properly after being downloaded so game cannot be played
*** For all of you that are having problems with “necemem.sni not found” ***
This seems to be different for everyone and I couldn’t find a fix that worked for me online. What I ended up figuring out on my own was that I had two files “lcsebody.” and “soundpacksevo.”. The fact that these ended in a period with no actual extension did really weird things to my computer. For instance I still can’t delete the files for some reason. What solved the problem for me was changing the names of these to the same thing without the period. The problem is windows wont actually let you. Luckily it appears you can change it as long as you do it in the zip file itself. I used the Winrar trial and was able to do this by simply opening the zip and right clicking the file and choosing rename.
Hope this helps someone who was as confused as me!
Hey, I don’t know if you’re notice a question after all this time but I can hope. The game works great, if with some of the text awkwardly spaced, for like two minutes into the game. The moment I enter the boss dungeon, the game freezes completely, and I’m stuck with not being able to click anything and no text, just the background of the boss dungeon. Any idea why this happens? I even turned off showing effects.
“This game failed to generate a directinputmanager” that is what I keep getting and I am no clicking on the desktop
i have downloaded the game but it is showing that ‘necemem.sni not found’ how can i fix that?
please tell me
Ok, so I downloaded this game and as some of the people above me, I am receiving an error message about the NECEMEM,SNI not being found. The fix that has been suggested for this is to change the name of the folder to HaremParty, however, when I downloaded it, the folder was already named HaremParty the star doesn’t seem to be part of the name anymore, so that is not the issue, if someone could please help me with this issue I would appreciate it.
To those with problem with NECEMEM.SNI, just change the folder name to something random, run the game, then change back to the name you want.
I already did but somehow it doesn’t work
My Harem party freezes up at certain points and won’t work help me please!
need help when i extracted all the parts and started the game it said necemem.sni not found what do i do need help
necemem.sni problem how i can deal with it????
Thanks admins, I appreciated your hardwork 🙂
and just to add, I also had problem with the text. It overlapping each other, but It already fixed after I copied Vera Fonts to game folder 🙂
I keep trying to save so I can continue, but as soon as I close the game I can’t access my save files due to some reason (C:\Users\NAME\Desktop\Harem Party-part1.rar:Cannot modify volume) so I have to restart it again :/ Which takes forever
Never mind It’s fixed
Thanks for the text wrap fix, admin. I appreciate the help.
when i extract the file isebody is broken
what is it ? necemem.sni not found
This game failed to generate a directinputmanager. Any help please admin and peoples?
I fixed this by attaching a keyboard to my device. This happened to me when I used a Windows tablet. Tried it on my laptop and worked fine. My tablet comes with a detachable keyboard with touchpad and when I connected that, the error was fixed.
Hey , just curious but.. shouldn’t there be an option to replay scenes or view CG or listen to the OST? if i remembered correctly the japanese version had it.. is it just me or does the english version do not have the options? thanks!
Seems like there is no gallery or replay scenes option in the game which makes this disappointing. Lets hope there will be a patch or something to add those options in the game.
so how come on some like harem oparty and do you like horny bunny we cant change the name or move the file or else it won’t work?
first time to ever play but cannot because it keeps saying NECEMEM.SNI is not found and the game failed to set NECEMEM.SNI
So mine is constantly pulling u errors did I download it incorrectly some how because I’ve noticed that some of the parts are the same
היי האם אתם יודעים שמומלץ לעשות מנוי ל מאמן כושר אישי, מאמן כושר אישי, מגיע/ה אליך פעמיים בשבוע. מומלץ לפעילות גופנית, בונה לך תוכנית כושר אישית שמתאימה לך לאופי שלך
Is there any way to fix the word wrap? I installed the fonts from Koihime Musou, but that didn’t fix it, any way to fix?
My Game keeps freezing at certain points, I got past some but it keeps freezing and I have to quit the game eventually. Any Help?
Is there a fix for the text run off?
I have read through the information in the Installation/Error troubleshooting section, installed the font, but as with others the text still is not running off the screen. Is there another fix?
when downloading part 4 it says expired after pressing the download button
i need help fixing the text run off. i already have the fonts installed but its not working
how can i fix that problem????
Seems to just repeat a “necemem.sni not found” error.
found the same problem
just run the program as admin. and play
do we need to ‘extract here’ part by part, or u can just extract all of them?
Just first one.
Hi, I`ve just download all parts but part 8 is missing and the “soundpacksevo” data is broken please help!
It seems that the game work fine but the “soundpacksevo” is broken can u upload the data pls ?
Seems to just repeat a “necemem.sni not found” error.
u need to copy contents to a new folder, like ”HaremParty” and then try again
changing game main folder name to “HaremParty” worked
thx
nice one admin,keep up ur good work =)
So u only need to download the first part?
they are separated into part files… the extraction process will automatically extract the other parts to play.
any way to fix text runoff?
You don’t have font that mangagamer is using installed. I think it was posted on “Koihime musou” download page. gotta add it to this installation instructions later i guess…
I just tried installing those fonts and it didn’t fix the text runoff for Harem Party.
But where can i download it?
It worked just fine for me! Thanks Admin!
It does fix the text problem for me
Thank admin